Análisis de Regresión

Análisis de Regresión

Introducción

A medida que desarrolle diagramas de Causa y Efecto basados ​​en datos, tal vez desee examinar el grado de correlación entre las variables. 

Una medición estadística de la correlación se puede calcular utilizando el método de mínimos cuadrados para cuantificar la fuerza de la relación entre dos variables. El resultado de ese cálculo es el Coeficiente de Correlación, o (r), que oscila entre -1 y 1. Un valor de 1 indica una correlación positiva perfecta: a medida que aumenta una variable, la segunda aumenta de forma lineal. Del mismo modo, un valor de -1 indica una correlación negativa perfecta: a medida que aumenta una variable, la segunda disminuye. Un valor de cero indica una correlación de cero.

Antes de calcular el coeficiente de correlación, el primer paso es construir un diagrama de dispersión. Mirar el diagrama de dispersión le dará una amplia comprensión de la correlación. A continuación se muestra un ejemplo de gráfico de dispersión basado en un fabricante de automóviles.

En este caso, el equipo de mejora de procesos está analizando los esfuerzos de cierre de puertas para comprender cuáles podrían ser las causas. El eje Y representa el ancho de la brecha entre la brida de sellado de la puerta de un auto y la brida de sellado en el cuerpo, una medida de cuán apretada está ajustada la puerta al cuerpo. El diagrama de espina de pescado indicó que la variabilidad en la brecha del sello podría ser una causa de variabilidad en los esfuerzos de cierre de puertas.

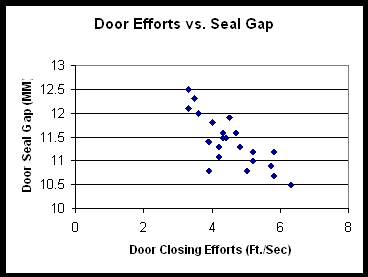
En este caso, puede ver un patrón en los datos que indica una correlación negativa (pendiente negativa) entre las dos variables. De hecho, el coeficiente de correlación es -0.78, lo que indica una fuerte relación inversa o negativa.

Nota: Es importante tener en cuenta que la correlación no es causa: dos variables pueden estar muy correlacionadas, pero ambas pueden ser causadas por una tercera variable. Por ejemplo, considere dos variables: A) cuánto crece mi pasto por semana y B) la profundidad promedio del reservorio local. Ambas variables podrían estar altamente correlacionadas porque ambas dependen de una tercera variable: cuánto llueve.

En el ejemplo de la puerta de nuestro automóvil, tiene sentido que cuanto más apretado sea el espacio entre las superficies de sellado de chapa metálica (antes de agregar burletes y adornos), más difícil será cerrar la puerta. Entonces, un entendimiento rudimentario de la mecánica apoyaría la hipótesis de que existe una relación causal. Otros procesos industriales no siempre son tan obvios como estos ejemplos simples, y la determinación de relaciones causales puede requerir una experimentación más extensa (Diseño de Experimentos).

Análisis de Regresión Simple

Si bien el Análisis de correlación no asume una relación causal entre las variables, el Análisis de regresión supone que una variable depende de: A) otra variable independiente única (Regresión simple) o B) múltiples variables independientes (Regresión múltiple).

La regresión traza una línea de mejor ajuste a los datos utilizando el método de mínimos cuadrados. Puede ver un ejemplo a continuación de regresión lineal utilizando el mismo diagrama de dispersión de la puerta del automóvil:

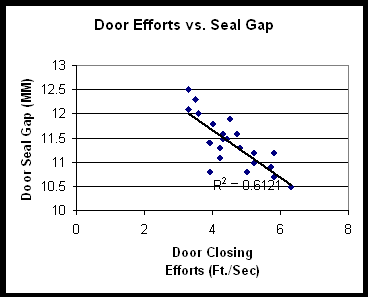
Puede ver que los datos están agrupados cerca de la línea y que la línea tiene una pendiente descendente. Hay una fuerte correlación negativa expresada por dos estadísticas relacionadas: el valor de r, como se indicó anteriormente es, -0.78 el valor de r2 es, por lo tanto, de 0.61. R2, llamado el Coeficiente de Determinación, expresa qué tanto de la variabilidad en la variable dependiente se explica por la variabilidad en la variable independiente. Puede encontrar que una ecuación no lineal, como una función exponencial o de potencia, puede proporcionar un mejor ajuste y obtener un r2 más alto que una ecuación lineal.

Análisis de Regresión Múltiple

El análisis de regresión múltiple utiliza una metodología similar a la regresión simple, pero incluye más de una variable independiente. Los modelos econométricos son un buen ejemplo, donde la variable dependiente del PBI se puede analizar en términos de múltiples variables independientes, como las tasas de interés, el crecimiento de la productividad, el gasto gubernamental, las tasas de ahorro, la confianza del consumidor, etc.

Muchas veces, los datos históricos se utilizan en regresión múltiple en un intento por identificar las entradas más importantes para un proceso. El beneficio de este tipo de análisis es que puede hacerse de manera muy rápida y relativamente simple. Sin embargo, hay varias trampas potenciales:

• Los datos pueden ser inconsistentes debido a los diferentes sistemas de medición, la variación de calibración, los diferentes operadores o los errores de registro.
• El rango de las variables puede ser muy limitado y puede dar una indicación falsa de baja correlación. Por ejemplo, un proceso puede tener controles de temperatura porque en el pasado se ha encontrado que la temperatura tiene un impacto en la salida. Por lo tanto, el uso de datos históricos de temperatura puede indicar poca importancia porque el rango de temperatura ya está controlado en una tolerancia estricta.
• Puede haber un lapso de tiempo que influye en la relación; por ejemplo, la temperatura puede ser mucho más crítica en un punto temprano del proceso que en un punto posterior, o viceversa. También puede haber efectos de inventario que deben tomarse en cuenta para asegurarse de que todas las mediciones se tomen en un punto constante del proceso.

Una vez más, es fundamental recordar que la correlación no es causalidad. Como lo indican Box, Hunter y Hunter: "Hablando en términos generales, para descubrir qué sucede cuando cambias algo, es necesario cambiarlo. Para inferir con seguridad la causalidad, el experimentador no puede confiar en los acontecimientos naturales para elegir el diseño para él; elija el diseño por sí mismo y, en particular, debe introducir la aleatorización para romper los vínculos con posibles variables ocultas ". 1

Regresando a nuestro ejemplo de esfuerzos de cierre de puertas, recordará que la brecha del sello de la puerta tuvo un r2 de 0.61. Usando la regresión múltiple, y agregando la variable adicional "durómetro de sellador de puerta" (suavidad), el r2 se eleva a 0.66. Así que el durómetro del sellador de la puerta agregó algo de poder explicativo, pero mínimo. Analizado individualmente, el durómetro tuvo una correlación mucho menor con los esfuerzos de cierre de la puerta: solo 0.41.

Este análisis se basó en datos históricos, por lo que, como se señaló anteriormente, el análisis de regresión solo nos dice qué impacto tuvo en los esfuerzos de la puerta, no qué impacto podría tener. Si el rango de mediciones del durómetro fue mayor, podríamos haber visto una relación más fuerte con los esfuerzos de cierre de puertas y una mayor variabilidad en la salida.


1. George E. P. Box, William G. Hunter y J. Stuart Hunter, Statistics for Experimenters - Introducción al diseño, análisis de datos y construcción de modelos (John Wiley and Sons, Inc. 1978) Página 495.

Resumen

La herramienta de análisis de regresión es una herramienta avanzada que puede identificar cómo se relacionan las diferentes variables en un proceso. La herramienta de regresión le dirá si una o varias variables están correlacionadas con una salida de proceso. Esta información puede identificar dónde se necesita el control del proceso o qué factores son el mejor punto de partida para un proyecto de mejora del proceso.

Fuente: https://www.moresteam.com/toolbox/regression-analysis.cfm